数学：复利原理，排列组合原理，费马帕斯卡系统

统计学：高斯分布

物理学：平衡，临界质量

生物学：进化论。复杂适应系统

工程学：后备系统，断裂点理论

社会科学：自我组织理论，层次进化理论。艾尔法罗预判模型

心理学：误判心理学

复利原理

爱因斯坦说过这么一句：

“Compound interest is the eighth wonder of the world. He who understands it, earns it … he who doesn’t … pays it.”

翻译过来：复利是世界第八大奇迹。知之者赚、不知之者被赚。

复利，是世界运行的底层逻辑之一。

今天，我们就聊聊“复利”。

先说“利息”

利息，这个概念虽然简单，但人们普遍接受利息的存在，也就是近一百年内的事情。

在中国人的印象里，“利滚利”是缺德的，是地主恶霸做的事；

在西方人眼里，莎士比亚笔下的夏洛克代表着邪恶；

地球上绝大多数宗教，都有严格的教义，禁止收取利息。甚至，连善于理财的犹太人，他们的教义里都规定“不得向同族收取任何利息”。

随着经济学的发展，人们认识到：“利息”是最高效的调配资源方法。

哪里缺钱，哪里就出个高利息，自然就会有钱过去。

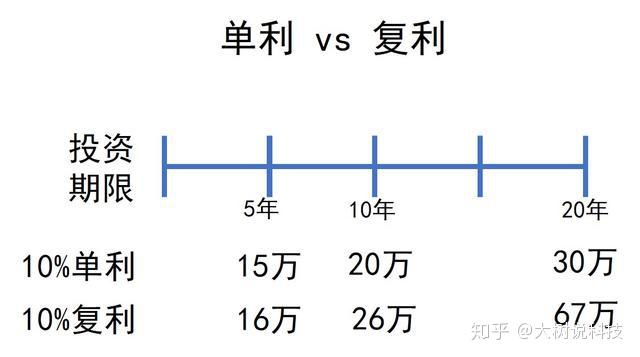
在利率的计算上面一般分两种：单利，复利。

所谓单利，就是本金固定，到最后一次性结算利息。

10万元，年利率为5%，借5年，最后的利息总和2.5万元，就是单利的算法。

你把钱存进银行，他们会给你利息，不过全世界绝大多银行都只支付单利，因为银行在占你便宜。

“复利”概念

复利，俗称“利滚利”，就是上一期的利息加入到下一期的本金。

单利的本金=初始本金

复利的本金=初始本金+上一期利息

如果对比单利与复利的收益率，你会发现，银行究竟占了你多少便宜。

只要能积累的东西，基本上最终都会产生复利效应。

那么，它的增长最终大抵是这样的：

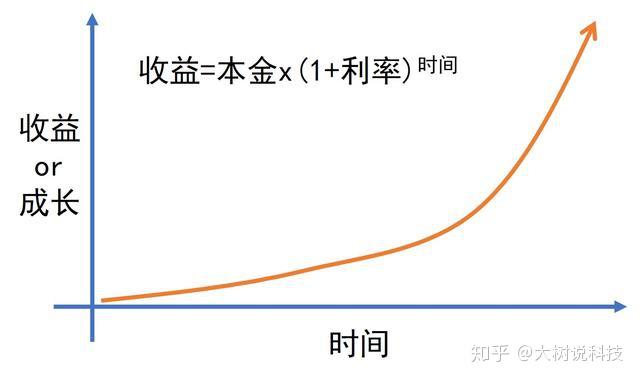
复利的构成

复利有两个基本要素：时间与利率

巴菲特说过：“人生就像滚雪球，关键是要找到足够湿的雪，和足够长的坡。”

湿的雪就是利率，长的坡就是时间。

（1）复利的时间

时间是一种的伟大力量

我们常常高估一天内可以做到的事情，却低估了一年里可以做到的事情。

据测算，假设20%的年化收益，10年变成6倍，20年变成39倍，50年将变成9100倍。

有人曾对1975-1982年美国股票市场上市值最大的500只股票进行统计。

这8年是股市的波动不大。

在1年的时间里，有3%的股票上涨了1倍，

时间拉长到3年，有18.6%上涨了1倍以上

5年，价格上涨超一倍的股票有38%。

换句话说，你买30支股票，一年里有可能1支股票翻倍，五年里会有10支以上翻倍，这就是时间的力量。

(2）复利的利率

利率很重要，但很多人容易忽视开始时的小收益而会选择放弃。

例如：1万块，年化10%利率计算，一年下来也也就1000收益，每天也就2元多一点，对很多人来说都没有多大的吸引力。

但做过投资的人知道，保持10%的年化收益率是多么困难。

股神巴菲特也才年化20%。

投资中有个72法则，即用72除以你的年化利率，得到的结果就是资产翻番所要的时间。

如果年化复合利率12%，资产翻番要6年，年化15%，资产翻番需要5年。

接受开始的进步很小这个事实，有助于对复利这个概念形成正确的期待，拥有足够的耐心等待复利效果的显现。

世界运行中的“复利”

（1）财富投资

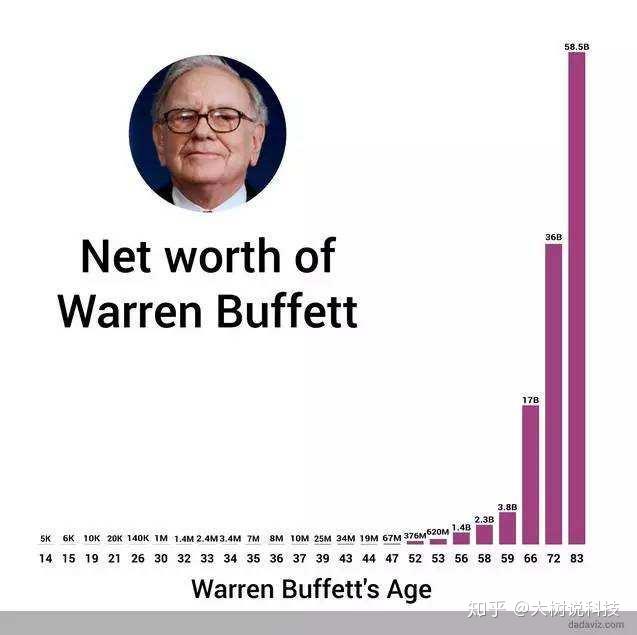
巴菲特一生中99%的财富都是他50岁之后获得的。

也就是说，50岁之前，他也是一个普通的中产阶级。

从27岁，他投资的年复利是20%，50岁之后，进入财富爆炸期，靠的就是时间和复利的力量。

（2）个人成长

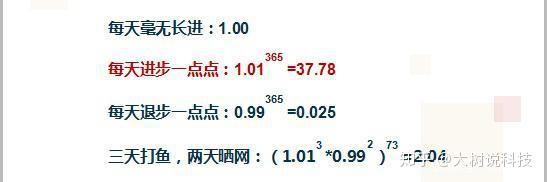
个人的成长也同样符合复利增长曲线。

无论是读书、锻炼或者学习某一个知识。只要是积累型的操作，都会接着复利的力量，完成个人的蜕变。

（3）历史进程

正如上文所说：在任何可以积累的系统里，都存在“复利”。

这种曲线在很多地方都是一样的

世界人口增长曲线也是这样的：

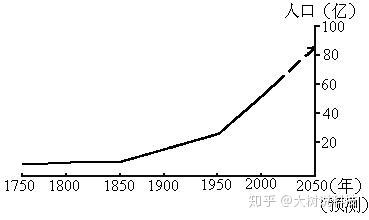
道琼斯指数过去一百年的增长曲线也如此：

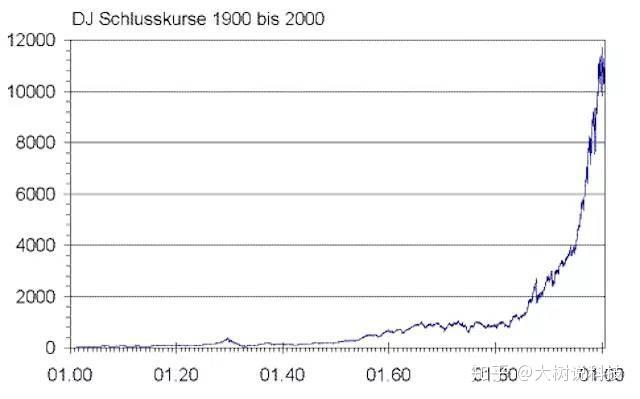
科学技术也是如此：

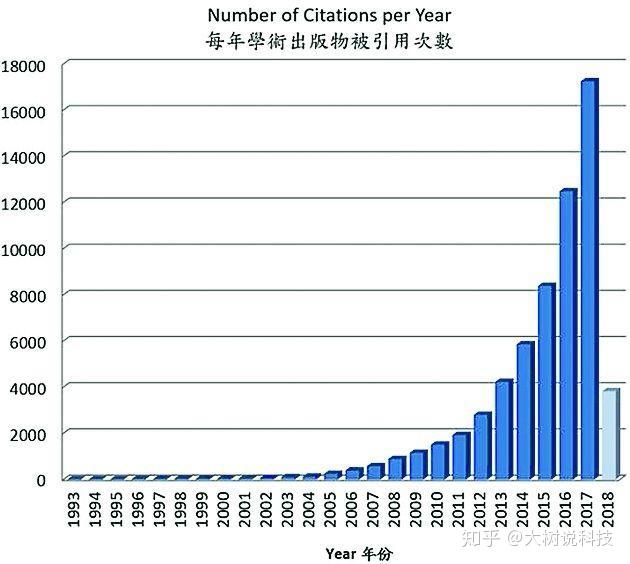
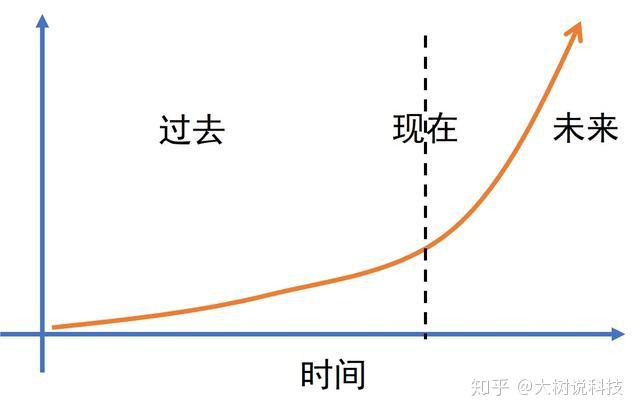
其实，我们正站在人类社会发展的拐点上，经过漫长的积累，人类社会正在进入高速发展期。

因此，我们在对未来进行评估时，不能根据过去的经验。

因为未来的发展，会远超我们对现在的认知。

总结

（1）复利，是世界运行的底层逻辑之一。

（2）在任何可以积累的系统里，都存在“复利”。

（3）在财富投资与个人成长中，相信时间的力量，坚守复利原则。

（4）预测未来，要有“复利”的视角。

费马帕斯卡系统

一、什么是费马帕斯卡系统？
故事起源：

说起概率论起源的故事，就要提到法国的两个数学家。一个叫做帕斯卡，一个叫做费马。

帕斯卡是17世纪有名的“神童”数学家。费马是一位业余的大数学家，许多故事都与他有关。

帕斯卡认识的朋友中有两个是赌徒。 1651年，法国一位贵族梅累向法国数学家、物理学家帕斯卡提出了一个十分有趣的“分赌注”问题。这两个赌徒说，他俩下赌金之后，约定谁先赢满5局，谁就获得全部赌金。赌了半天， A赢了4局， B赢了3局，时间很晚了，他们都不想再赌下去了。那么，这个钱应该怎么分？是不是把钱分成7份，赢了4局的就拿4份，赢了3局的就拿3份呢？或者，因为最早说的是满5局，而谁也没达到，所以就一人分一半呢？这两种分法都不对。

正确的答案是：赢了4局的拿这个钱的3／4,赢了3局的拿这个钱的1／4。为什么呢？假定他们俩再赌一局，或者 A赢，或者 B赢。若是 A赢满了5局，钱应该全归他； A如果输了，即 A、 B各赢4局，这个钱应该对半分。现在， A赢、输的可能性都是1／2,所以，他拿的钱应该是1／2×1＋1／2×1／2＝3／4,当然， B就应该得1／4。这个问题可把他难住了，他苦苦思考了两三年，到1654年才算有了点眉目。于是他写信给的好友费马，两人讨论结果，取得了一致的意见：不应该按已经完成的赌局盘数来计算赌注分配，而是应该把目光放在赌局中断时，后面应该继续进行的盘数上。

梅累的分法是对的，他应得64个金币的，赌友应得64金币的。

所以，已经完成的盘数不重要，重要的是赌徒们如果要最终赢得赌局，需要去完成的盘数。

通过这次讨论，开始形成了概率论当中一个重要的概念—————数学期望。

在上述问题中，数学期望是一个平均值，就是对将来不确定的钱今天应该怎么算，这就要用A赢输的概率1／2去乘上他可能得到的钱，再把它们加起来。概率论从此就发展起来，今天已经成为应用非常广泛的一门学科。

二、帕斯卡三角
费马假设：费马和帕斯卡一起玩抛硬币游戏，每一次【头】（head）和【尾】（tail）的概率都是1/2。两人各出50法郎做赌注。规则是：先赢10盘就能赢得100法郎。抛硬币是【头】，费马赢，记为「h」；如果是【尾】，则帕斯卡赢，记为「t」。

赌局进行到{ 费马8 ：帕斯卡7 }的时候，这个赌局需要提前结束。该怎么公平分100法郎呢？

帕斯卡发现，可以用他发现的「帕斯卡三角」来解「赌注分配问题」。

这个三角形的「塔尖」是一个「1」，这一行称为「0」行。下面依次是1、2、3、4、5、6…行。每一行的左右两边数字都是1，每行里的数字是它上面两个数字之和。

我们回到费马和帕斯卡那个抛硬币的赌局里。8 - 7，刚才说了，还需要4盘才能决出胜负。好，我们看上图中的第4行，「1,4,6,4,1」。

这里有一点值得注意：费马现在赢了8局，再赢2局即可赢得赌局。那么前两个数字「1,4」就代表了帕斯卡赢的概率；同理，帕斯卡需要再赢3局——>可推：「6,4,1」则代表了费马赢的概率。

前面算过，最后4盘有16种不同的结果，正好是「1+4+6+4+1=16」。费马赢的概率：6+4+1=11，11/16=68.75%。帕斯卡的概率为 1-费马赢的概率。

帕斯卡三角
总结
就如查理.芒格所言：

如果你没有把这个基本的，但有些不那么自然的基础数学概率方法变成你生活的一部分，缺乏数学运算能力，在我们大多数人所过的生活中，你们将会像一个参加踢屁股比赛的独腿人。这等于将胜利拱手他人。

因此我们需要学好用好概率论来帮助我们做出最大概率获胜的决策。

正态分布

统计学里面，正态分布（normal distribution）最常见。男女身高、寿命、血压、考试成绩、测量误差等等，都属于正态分布。

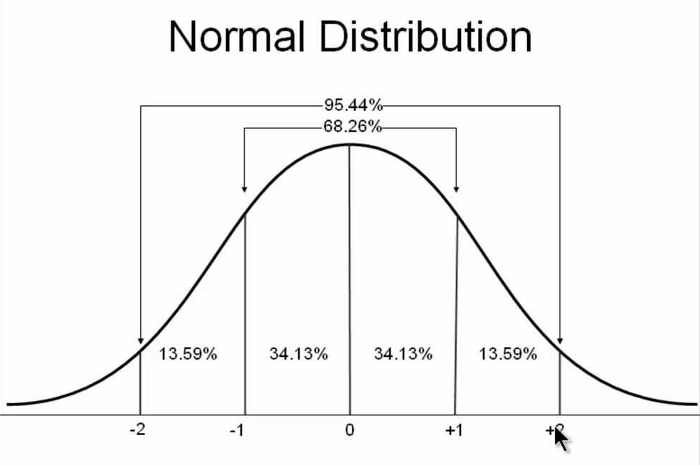
以前，我认为中间状态是事物的常态，过高和过低都属于少数，这导致了正态分布的普遍性。最近，读到了 John D. Cook 的文章，才知道我的这种想法是错的。

正态分布为什么常见？真正原因是中心极限定理（central limit theorem）。

“多个独立统计量的和的平均值，符合正态分布。”

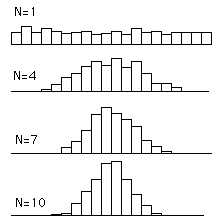
上图中，随着统计量个数的增加，它们和的平均值越来越符合正态分布。

根据中心极限定理，如果一个事物受到多种因素的影响，不管每个因素本身是什么分布，它们加总后，结果的平均值就是正态分布。

举例来说，人的身高既有先天因素（基因），也有后天因素（营养）。每一种因素对身高的影响都是一个统计量，不管这些统计量本身是什么分布，它们和的平均值符合正态分布。（注意：男性身高和女性身高都是正态分布，但男女混合人群的身高不是正态分布。）

许多事物都受到多种因素的影响，这导致了正态分布的常见。

读到这里，读者可能马上就会提出一个问题：正态分布是对称的（高个子与矮个子的比例相同），但是很多真实世界的分布是不对称的。

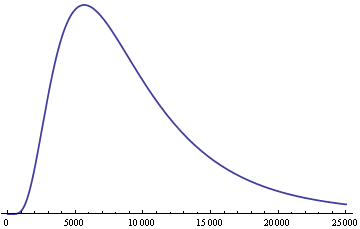
比如，财富的分布就是不对称的，富人的有钱程度（可能比平均值高出上万倍），远远超出穷人的贫穷程度（平均值的十分之一就是赤贫了），即财富分布曲线有右侧的长尾。相比来说，身高的差异就小得多，最高和最矮的人与平均身高的差距，都在30%多。

这是为什么呢，财富明明也受到多种因素的影响，怎么就不是正态分布呢？

原来，正态分布只适合各种因素累加的情况，如果这些因素不是彼此独立的，会互相加强影响，那么就不是正态分布了。一个人是否能够挣大钱，由多种因素决定：

家庭

教育

运气

工作

…

这些因素都不是独立的，会彼此加强。如果出生在上层家庭，那么你就有更大的机会接受良好的教育、找到高薪的工作、遇见好机会，反之亦然。也就是说，这不是 1 + 1 = 2 的效果，而是 1 + 1 > 2。

统计学家发现，如果各种因素对结果的影响不是相加，而是相乘，那么最终结果不是正态分布，而是对数正态分布（log normal distribution），即x的对数值log(x)满足正态分布。

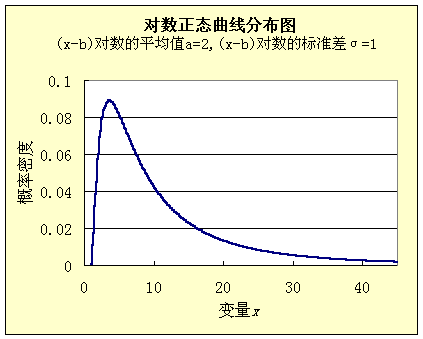
这就是说，财富的对数值满足正态分布。如果平均财富是10,000元，那么1000元～10,000元之间的穷人（比平均值低一个数量级，宽度为9000）与10,000元~100,000元之间的富人（比平均值高一个数量级，宽度为90,000）人数一样多。因此，财富曲线左侧的范围比较窄，右侧出现长尾。

临界质量

“物理学中的临界质量是一个非常强大的模型。”——查理芒格。

临界质量最早是在核物理学中，指的是维持核子连锁反应所需的裂变材料质量。引申到从量变到质变的拐点，也就是临界点。

在之前讲复利模型到时候就提到过临界点，说的是复利模型，有一个关键的要素就是达到临界点之后才能产生裂变式的指数增长。

临界点，也可以叫裂变阈值，说的是有些东西积累到一定程度，就有可能激发连锁反应，迅速扩张，形成裂变。我们可以用来理解世界非常重要的模型之一，很多现象都可以用这个模型来解释。

比如有的谣言经过少数人的传播，慢慢积累到一定程度之后，就会变成被普遍认可的谣言。比如小的时候的一个经典谣言，说是在月球上可以看到唯一一个地球的建筑就是长城。相信这个谣言，最开始是某些国家荣誉感爆棚的人编造的，但是慢慢的居然发酵成了一个被普遍认同的谣言。

再比如朋友圈的一些热点文章，即便它的标题一点都不吸引人，如果有三五个好友连续的转发了这篇文章，你也很可能就会点进去。所以朋友圈的爆文也是有一个临界点的，到达临界点之后才能得到广泛的传播。

再比如从众效应也是有一个临界点的，之前有人做过一个实验，就是一个街道有一群人向着一个方向跑，假装很慌张的样子，最开始向这个方向跑的人很少，然后实验的人数慢慢增多，到达某一个人说的时候，就会影响到周围的人，那些人本能的也会跟着这些人跑，然后跑的人越来越多，即使他们根本不知道他们为什么跑。

再比如新技术和某些产品的普及中，临界质量也是非常重要的。有些技术要用的人多到一定程度之后才有意义，比如说电话，如果电话不能用来打电话给其他人，那就没有意义。同样的，社交软件也是如此，如果你的社交软件里面没有好友，那就不是社交软件。如果一个线上社区没有人发内容，没有人评论，那么这个社区肯定也没有人能待下去。所以像微信、知乎这些产品增长过程中，都有很明显的临界点。

关于临界点，马尔科姆有一本书是《引爆点》，对这种思想进行了非常详细的阐述，并且得到了更多的例子。

当然除了解释现实生活中的一些现象临界点，也可以指导我们的一些行动。只要是可持续积累的，会产生连锁反应的，我们都要坚持积累，直到临界点的到来。

比如说学习，最开始学习的时候只有一些零散的知识点，但是一旦这些知识点积累到一定程度之后，他们之间就会形成关联，达到融会贯通的程度，再学相关的知识就会变得非常快，产生裂变反应。

同样的自己的关系网络，自己的资金，都可以积累到产生这种明显的连锁反应，但是很可能开始很长一段时间都是看不到回报的，必须撑到临界点之后。如果你知道这个模型，那么你就会更有信心，即便是在看不到回报的情况下也能坚持，因为你知道临界点终归有一天会到来。

复杂适应系统

系统论——复杂适应系统CAS（三） - 郝hai - 博客园

后备系统

工程学中，典型的工程冗余（rǒng yú）指的是向系统添加“额外”的关键组件，它是利用系统的并联模型来提高系统可靠性的一种手段，通常使用备份或者自动防故障装置。冗余也常被称为“多数表决系统”或“表决逻辑系统”。

在许多安全导向的系统上，比如飞机上的双引擎和液压系统，控制系统上的某些部件也许会被一式三份，专业术语：三重模块冗余（TMR）。一个部件出错将会被另外两个备份部件所取代。

冗余备份模型

在工程领域有很多这样的例子，从火箭的控制和动力系统，到数据中心大量使用的额外硬盘和备用电源。

一种常见形式的被动冗余是在桥梁上使用超高强度的钢桁和支柱。这种高强度能够允许一些部件的老化但不至于使桥垮塌。

互联网本身就是一个典型冗余实例，它的大多数核心传输网络和站点都被设计成可以抵御单个链接或节点的故障。

人体的听觉系统和视觉系统都是冗余备份的典型例子，视觉系统失去一只眼睛不至完全失明，但却会深深损害知觉。听力系统失去一只耳朵不至耳聋，但肯定会受到损害。性能下降是常常是跟发生少数失效的被动冗余关联在一起的。

冗余方案还可以添加到各种系统中，能够帮助我们避免灾难的发生。

一、工程以外的应用

冗余备份是查理芒格提到的一个重要模型，它源于工程学，但思路可以应用到很多领域。一旦你尝试给自己的生活增加稳定可靠性，就会找到很多这样的例子，例如：

越野车的备用轮胎
商场或公司里的发电机
跳伞的备用伞包
商业轮船上的多个精密计时器
软件的多版本编程系统
大厦的防火安全通道等等

冗余备份并不总是值得的

我们从上面的实例中不难得出关于冗余的两个特征:

向系统中添加冗余肯定会增加整个系统的成本。
在不同的系统，不同的场景中，失败带来的后果是不一样的。

考虑了这两点后，在向系统中添加冗余时，就要权衡增加它的成本和如果没有冗余机制所带来的后果。

如果系统中断，你会失去什么?
预防某种故障发生需要付出什么代价?
增加冗余的成本是否大于潜在的损失?

一旦你发现为系统增加冗余可以避免一些失败，就可能会不计成本的增加一些备份方案，但它们并不都是值得的。

例如美国总统和副总统同时访问同一地区，会安排分开乘机，如果只是一家上市公司的高管呢？

为家庭财务系统增加冗余

在日常生活中也有很多冗余方案的使用。我最喜欢的一个例子就是家庭财务的冗余应用。把你的家庭收入当做一个系统：

你是怎么赚钱的?

你有多少个收入来源?

如果主要收入出现问题，会发生什么?

假如你是双职工家庭的一员呢?若夫妻双方在同一个单位工作，情况会有什么不同?

我们通常不会对个人及家庭的收入使用冗余方案，但这一点其实值得我们去不断思考。

经常思考这些问题，就会强化思维，从而建立正确的思维框架。

断裂点理论

“零售引力规律”、“城市断裂点理论”和“价格断裂点理论”都查了,看完觉得跟“临界点理论”应该放在一起看，说的都是量变引起质变的极值问题，极值前后的结果截然不同。类比房价就是泡沫崩盘的价格极点；类比零售就是产品定价和销量预估的函数极值；类比生活就是做一件事，从过程看如果积累没达到断裂点，从结果看就不会产生明显变化。

自我组织理论

自组织 - 集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织

层次进化理论

层次进化理论是一个涉及多个学科的广泛概念，它探讨了复杂系统中不同层次结构的演变和发展。以下是层次进化理论的一些关键点：

定义与核心问题：
层次进化理论认为，复杂性以层级结构存在，层级是复杂性的必要条件。系统的层级进化问题就是复杂性不断生成的过程。
适应性层级进化思想：
复杂适应系统理论的进化思想可以概括为适应性层级进化思想，这是系统层级进化思想的重要组成部分。适应性层级进化思想体现为适应性主体相互作用的多级网络，基于主体的模型与模拟适应性进化的遗传算法，以及适应性景观与适应性进化过程。
适应性主体相互作用的多级网络：
适应性主体是在一定层次上收集有关周围环境以及它自己和自己行为的信息，然后加工与处理这些信息，并向环境输出信息和作用，从而适应环境的行为主体。适应性主体之间通过资源交换、信息流相互作用进化成多级网络。
基于主体的模型与模拟适应性进化的遗传算法：
对主体及其适应性进行建模，并创立了以综合进化论为基础的遗传算法。基于主体的模型和遗传算法为适应性层级进化的研究提供了科学基础。
适应性景观与适应性进化过程：
适应性层级进化思想强调个体在进化中的主动性以及以计算建模为主的研究方法。由于计算机模型同时具备理论和实验的特性，因此，计算建模为系统适应性层级进化思想的研究提供了科学基础。
层创进化：
层创进化是一种在20世纪初为摆脱生机论和机械论的论证而从科学和哲学角度提出的理论。通过进化，新的统一体可能“突生”，并呈现出一种从它们先前的角度不可能分析到的不可预料的特质，因此需要一种新的研究模式。

层次进化理论在理解复杂系统的结构和功能、以及这些系统如何随时间演变方面提供了重要的视角。它强调了个体和群体层面上的相互作用，以及这些相互作用如何导致新层次结构的出现和复杂性的增加。

埃罗预测法

埃罗预测法（Elo rating system）：埃罗预测法最初由美国物理学家埃洛·阿奇博尔德·哈里森（Elo Arpad Haraszti）在1960年代提出，用于评估国际象棋中棋手的实力。后来，杰奎斯·布莱克根据1500场英超比赛对埃罗法进行了改进和创新，并被广泛应用于各种竞技体育，包括足球，以评估球队或球员的相对实力。埃罗评分系统的核心公式如下： RA′=RA+K(SA−EA)R**A′=R**A+K(S**A−E**A) RB′=RB+K(SB−EB)R**B′=R**B+K(S**B−E**B) 其中，RAR**A 和 RBR**B 分别为比赛前球队A和球队B的评分，RA′R**A′ 和 RB′R**B′ 为比赛后更新的评分，SAS**A 和 SBS**B 为比赛结果（胜/负/平）对应的实际得分（通常为1/0/0.5），EAE**A 和 EBE**B 为比赛前预测的胜率，KK 是一个常量，决定了评分更新的幅度，通常取值为20或30

误判心理学

查理·芒格（Charlie Munger）在他的演讲和著作中详细阐述了人类误判心理学的概念，他提出了25个常见的心理倾向，这些倾向影响着人们的思考和行为，导致误判。以下是一些关键点：

奖励和惩罚超级反应倾向：人们对于奖励和惩罚的过度反应，这会影响他们的决策和行为。
喜欢/热爱倾向：人们倾向于忽略所爱对象的缺点，对其百依百顺。
讨厌/憎恨倾向：与喜欢/热爱倾向相反，人们会因为讨厌或憎恨某个事物而产生偏见。
避免怀疑倾向：人们不愿意陷入怀疑和不确定的状态中，总是想立即作出决定。
避免不一致性倾向：人们讨厌前后不一致，总想前后协调起来。
好奇心倾向：人们天生具有好奇心，这驱使他们探索未知。
康德式公平倾向：人们追求公平，这种倾向影响他们的决策。
艳羡/妒忌倾向：人们可能会因为他人的成功或拥有而感到妒忌。
回馈倾向：人们倾向于回报他人的好意或恶意。
受简单联想影响的倾向：人们可能会因为某个事物与另一个积极或消极的事物相联系而受到影响。
简单的、避免痛苦的心理否认：人们可能会否认痛苦的现实，以避免心理上的痛苦。
自视过高的倾向：人们往往高估自己的能力和拥有的物品的价值。
过度乐观倾向：人们往往过于乐观地评估未来事件的可能性和结果。
被剥夺超级反应倾向：人们对于即将失去的东西反应强烈。
社会认同倾向：人们倾向于模仿他们认同的群体的行为。